埃拉托斯特尼筛法

埃拉托斯特尼筛法，简称埃氏筛法，用来找出一定范围内所有的质数。

一、算法描述

1. 列出2及其以后的序列：2，3，4，5，6，7，8，……，n
2. 序列中第一个数字标为质数：2，3，4，5，6，7，8，……，n
3. 划掉后续序列中当前质数倍数的数字：2，3，4，5，6，7，8，……，n
4. 重复2-3步骤，直到当前质数的平方大于等于序列的最大数字，跳出2-3循环，进入5步骤
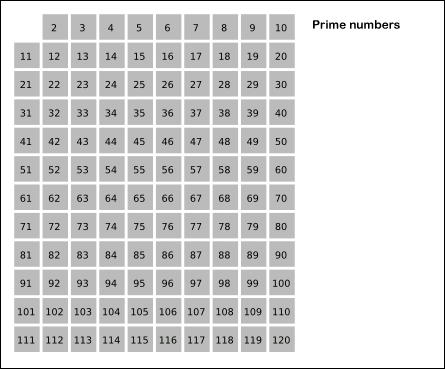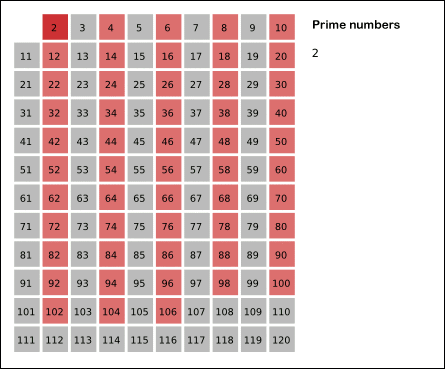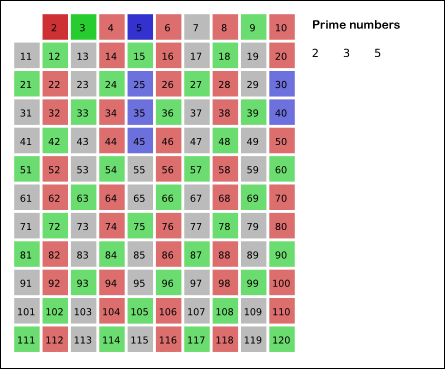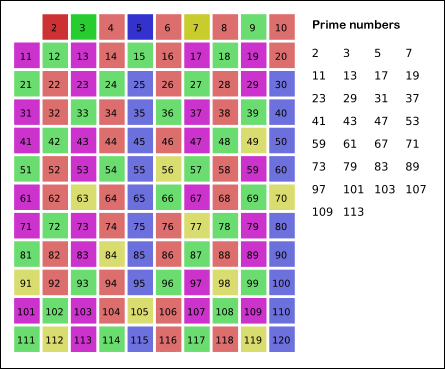
5. 剩余数字均标记为质数

二、代码实现

Python

def eratosthenes(n):
    IsPrime = [True] * (n + 1)
    for i in range(2, int(n ** 0.5) + 1):
        if IsPrime[i]:
            for j in range(i * i, n + 1, i):
                IsPrime[j] = False
    return {x for x in range(2, n + 1) if IsPrime[x]}

if __name__ == "__main__":
    print(eratosthenes(120))

Java

public class Eratosthenes {
    public static void solution(int n) {
        int[] prime = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            prime[i] = i;
        }
        for (int i = 2; i <= Math.pow(n, 0.5)+1; i++) {
            for (int j = i+i; j <= n; j += i) {
                prime[j] = 0;
            }
        }
        for (int i = 2; i <= n; i++) {
            if (prime[i] != 0) {
                System.out.print(prime[i] + " ");
            }
        }
    }

    public static void main(String[] args) {
        solution(120);
    }
}