编码、摘要与加密

编码（encoding）

编码本质是信息形式的转化，譬如十进制到二进制是一种编码。编码是一种双向转化，原始信息通过编码可以得到编码信息，编码信息通过解码可以得到原始信息。（有损编码除外）编码是一对一的。

例如：Base64，zip

摘要（digest）

摘要是通过哈希函数对任意大小的信息/数据生成固定大小的摘要信息。摘要是一种单向转化，原始信息通过摘要可以生成唯一的哈希值，但无法从摘要还原出原始信息。摘要是多对一的，即可能存在多个原始数据对应同一个摘要。

例如：MD5，SHA

加密（encryption）

加密是将明文信息转化为难以读取的密文内容，使之不可读。加密是一种双向转化，原始信息通过加密密钥转化为加密信息，加密信息通过解密密钥被还原为原始信息。加密是一对一的。加密密钥与解密密钥一致的加密方法称为对称加密；反之，加密密钥与解密密钥不一致的加密方法称为非对称加密。非对称加密的密钥分别称为公钥（public key）与私钥（private key）。

例如：AES，DES，RSA

一、编码：Base64

Base64是一种典型的编码。通常用在小图像的处理上，把二进制的图像文件转为文本，在网页上显示时再从文本转为图像，方便传输。

典型的例子还有迅雷的专用下载链接：thunder://QUFtYWduZXQ6P3h0PXVybjpidGloOkM5MUExNEIwRjBEMDZDRUM3MzUwQjRERUJFOTFBNTI5MzU4Nzg5QjNaWg==，也是Base64编码后的。

原理

Base64用64（2^6）个字符来表示任意二进制数据。

所有类型的文件，无论什么格式从计算机角度来看，都可以看成是二进制的文件。所以理论上任何文件、字符串都可以通过Base64进行编码。

具体原理：

建立一个64长度的字符数组，作为码表。
对要编码的数据进行3字节转4字节处理，每次顺序取数据的3个字节，共计3*8=24位，然后每6位进行高位补零得到4个新字节。

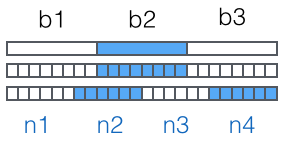
base64

由于数据长度不一定是3的整数倍，因此需要在数据的末尾补充\x00保证数据按照3的倍数对齐，每补一个\x00，编码后的字符串就会相应增加一个=用以表示补了多少字节，在解码的时候根据=的个数减去末尾的字节。
从3字节到4字节转化完成后，再查码表把字节转为字符，由于转化后的字节只有低6位有效，所以只需要一个64（2^6）长度的码表就可以满足查表的要求。

例子

  
import base64

# 读图像
with open('base64-sample.jpg', 'rb') as f:
    # 读字节
    data = f.read()
    print(len(data))
    print(data)
    # base64编码
    encode_data = base64.b64encode(data)
    print(len(encode_data))
    print(encode_data)

以上代码：

打开图像读取字节
进行base64编码
打印编码后的字符。

在chrome浏览器地址栏输入：data:image/jpg(图片的格式);base64,base64字符串，就可以直接从浏览器中看到图像。

二、摘要算法

摘要算法又称哈希算法、散列算法。它通过一个函数，把任意长度的数据转换为一个长度固定的数据串。

f(data) = digest，摘要算法可以理解为f()，其中digest长度为固定值。

摘要算法特性：在已知f()的情况下，由f(data)正向推出digest非常容易，但由digest逆向推出data则为不可解。因此摘要为单向。

常见的摘要算法：

MD5 Message Digest Algorithm 5，流行度极高，在很多文件下载校验中使用，但目前被发现存在碰撞冲突风险；任意长度输出为128bit=16字节摘要

SHA1 SHA：Security Hash Algorithm，由美国国家安全局NSA设计的安全散列算法系列； SHA1输出长度为160bit=20字节摘要

SHA256 继SHA1出现的算法(属于SHA-2类)，安全性较SHA1更高； SHA256输出长度为256bit=32字节摘要。

例子

MD5、SHA1、SHA256对hello world!进行摘要算法，分别得到32、40、64位的16进制字符串，乘以4就分别是：128bit、160bit、256bit。

  
import hashlib

md5 = hashlib.md5()
md5.update('hello world!'.encode('utf-8'))
sha1 = hashlib.sha1()
sha1.update('hello world!'.encode('utf-8'))
sha256 = hashlib.sha256()
sha256.update('hello world!'.encode('utf-8'))

print('md5: {}, sha1: {}, sha256: {}'.format(md5.hexdigest(), sha1.hexdigest(), sha256.hexdigest()))
print('md5: {}, sha1: {}, sha256: {}'.format(len(md5.hexdigest()), len(sha1.hexdigest()), len(sha256.hexdigest())))

md5: fc3ff98e8c6a0d3087d515c0473f8677, sha1: 430ce34d020724ed75a196dfc2ad67c77772d169, sha256: 7509e5bda0c762d2bac7f90d758b5b2263fa01ccbc542ab5e3df163be08e6ca9
md5: 32, sha1: 40, sha256: 64

应用

文件传输，发送方分别发出数据文件和摘要信息并公布摘要算法，接收方接收到数据文件后使用相同的摘要算法对数据文件进行验证，看是否为相同的摘要信息。
密码加密，用户登陆密码一般不以明文存储在数据库中，一方面是防止运维人员干坏事，另一方面是避免数据库被入侵后用户密码暴露。因此，在用户注册时对用户密码进行摘要处理得到摘要信息，再将摘要信息录入数据库就可以避免明文密码的暴露风险。而在用户登陆时额外要做的，只是再对用户输入的密码进行一次摘要处理。

碰撞

摘要算法把无限的数据集（无长度限制）映射到一个有限的摘要集（摘要长度限制），必然存在碰撞的情况，即不同的数据生成了相同的摘要。虽然常见几种算法设计都很好的避免了这种情况，但并不代表不会发生。从安全的角度来说，同时使用两种摘要算法可以把碰撞出现的概率减小到不计。

加盐 salt

摘要算法理论上无法逆向从摘要推出数据，但并不代表完全无法破解。把常见的数据/信息/密码等，先正向通过摘要算法生成摘要，并做成数据-摘要一一对应的彩虹表，那么拿到摘要信息后在彩虹表中进行检索就可以获取到原始数据/信息/密码。

加盐就是为了防止这种情况。加盐的摘要算法是：f(data + salt) = digest。计算某一数据的摘要时，根据不同口令（salt）计算出不同的摘要。要验证哈希值，必须同时提供正确的口令（salt），而口令（salt）是黑客无法提前获知的。

Hmac

Hmac是一个标准的加盐算法

  
import hmac

data = b'Hello, world!'
salt = b'secret'
h = hmac.new(salt, data, digestmod='MD5')
print(h.hexdigest())

fa4ee7d173f2d97ee79022d1a7355bcf

三、加密算法

加密是把明文转为密文，使数据/文件/信息变为不可读，或者说加密算法使得数据/文件/信息加密后得到的密文在直接读取的情况下无意义。同时，加密算法还要保证加密可逆，即在拥有密钥的情况下，可以从密文得到原文。

加密算法分为对称加密和非对称加密。对称加密：加/解密的密钥相同。非对称加密：加/解密的密钥不同，有私钥、公钥之分。常见的对称加密算法：AES、DES。常见的非对称加密算法：RSA。

加解密使用相同密钥：

对称加密

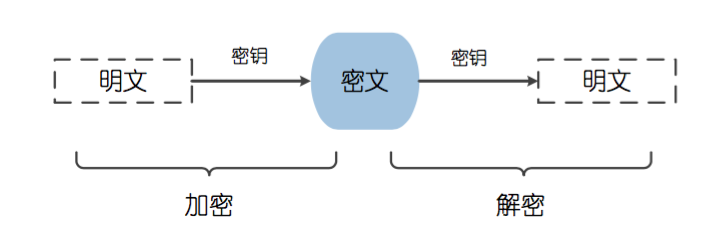
公钥加密-私钥解密或者私钥加密-公钥解密：

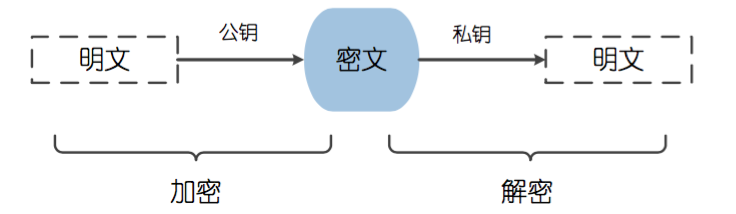
非对称加密

DES

DES：Data Encryption Standard，数据加密标准。

DES现在已经不是一种安全的加密方法，主要因为它使用的56位密钥过短。
DES作为一个标准已经被高级加密标准（AES）所取代。

AES

AES：Advanced Encryption Standard，高级加密标准。

AES已然成为对称密钥加密中最流行的算法之一。

RSA

RSA是一种非对称加密算法。非对称加密也叫公开密钥加密。

阮一峰的这两篇博文把RSA解释的非常通透了。只需要理解几个基本概念和定理就可以看懂。

RSA算法原理（一）

RSA算法原理（二）

互质，欧拉函数，费马小定理，欧拉定理，模逆元

RSA概念

非对称加密可以这样理解：private(public(x))=y，public(private(x))=y，使用public密钥加密的数据只可以通过private密钥解密，使用private密钥加密的数据只可以通过public密钥解密。

对称加密算法的一个最大弱点在于：密钥只有一套，加解密都使用同一套密钥，加密方需要把密钥告诉给解密方。当加解密双方处在不安全的网络环境时，密钥的暴露就会导致加密信息泄露。

非对称加密算法的优点在于：密钥有两套，加解密双方各持一套密钥。

A生成两套密钥(公钥、私钥)，私钥由A自己保存，公钥是公开的；
B获得A发布的公钥，将数据使用公钥加密，并将加密后的密文secret发出；
B处于不安全的网络环境中，B发出的密文secret不仅传给了A，网络中的黑客C也同时截获了密文secret；
收到密文secret后，由于C没有私钥，因此他无法解密secret；
收到密文secret后，A通过自己持有的私钥解密了secret，同时私钥只在本地保存未经过网络传输，因此私钥安全性非常高；
如果B在发出密文secret后，丢失了原数据，那么B的处境将会与C一样，无法通过破解密文secret得到原数据。

RSA生成过程

  
取两个大质数p、q；
计算r（φ(N)），N=p*q，φ(N)=φ(p)φ(q)=(p-1)(q-1)；
随机选取e，e需与r互质；
计算d，d是e关于r的模逆元，ed≡1(mod r)
(N，e)为公钥，(N，d)为私钥

RSA可靠性

RSA可靠性 = 已知公钥N、e，计算私钥d

  
ed≡1(mod r)，公钥中e，要计算d还需要知道r；
r=φ(N)=φ(p)φ(q)=(p-1)(q-1)，要计算r，需要知道p、q；
N=p*q，将N因式分解才能得到p、q

因此，破解RSA等价于：对N进行因数分解。

大整数的因数分解，是一件非常困难的事情。目前，除了暴力破解，还没有发现别的有效方法。

维基百科：

　　对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。
　　假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。
　　只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。

RSA加密算法，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

RSA加解密及证明

  
# 加密，公钥(N，e)。data的e次幂对N取余，且data必须小于N。
data^e ≡ secret (mod N)

# 解密，私钥(N，d)。secre的d次幂对N取余。
secret^d ≡ data (mod N)

# 证明
1. 由 data^e ≡ secret (mod N) 可以推出 secret = data^e - k*N
2. 将1式代入可得：secret^d = (data^e - k*N)^d
3. 将2式去括号可得：secret^d = data^ed - k*N^d
4. 由 ed ≡ 1 (mod r) 可以推出 ed = 1 + Kr
5. 将4式代入2式可得：secret^d = data^(1+Kr) - k*N^d
只需证明：data^(1+Kr) ≡ data (mod N)，即可证明：secret^d ≡ data (mod N)

# 证明：data^(1+Kr) ≡ data (mod N)
data与N互质时：
	1. 根据欧拉定理：data^r ≡ 1 (mod N)
	2. 由1式可得：data^Kr ≡ 1 (mod N)
	3. 由2式可得：data^(1+Kr) ≡ data (mod N)
data与N非互质时：
	1. 由于N由两个质数p、q相乘得到，因此N只有p、q两个因数，若data与N非互质，则data必为p或q的整数倍
	2. 由1可得：data = xp 或者 data = yq，且x与q互质、y与p互质(因为data < N，所以x一定小于q，所以x一定与q互质)
	3. 以 data = xp 为例，此时data与q互质且q为质数，根据欧拉定理：data^(q-1) ≡ 1 (mod q)
	4. 由3式可得：date^((q-1)*K(p-1)) ≡ 1 (mod q)
	5. 因(q-1)*K(p-1) = r，由4式可得：data^Kr ≡ 1 (mod q)
	6. 将5式分解可得：data^Kr = 1 + tq
	7. 将3的条件：data = xp 代入6式，可得：xp^Kr = 1 + tq，进一步可得：xp^(1+Kr) = xp + txpq
	8. 将3的条件：xp = data 代入7式，可得：data^(1+Kr) = data + tx*N
	9. 由8式可得：data^(1+Kr) ≡ data (mod N)

以上，给出了RSA的加解密过程，并进行了证明。需要注意的是：RSA加密的数据必须是整数且数据值必须小于N，之所以要小于N，是因为在data与N非互质的证明中，需要用到第3条data与q互质，而data与q互质的前提是第2条：data = xp，data < N。

编码、摘要与加密

一、编码：Base64

原理

例子

二、摘要算法

例子

应用

三、加密算法

DES

AES

RSA

RSA概念

RSA生成过程

RSA可靠性

RSA加解密及证明

Further Reading

数字签名

网络协议

自由软件与开源许可